Nederlands Tijdschrift voor Natuurkunde

Al ruim een halve eeuw is bekend dat germanium de beste eigenschappen heeft voor de ontwikkeling van informatietechnologie. Het was mede daarom het materiaal waarin de eerste transistors en geïntegreerde schakelingen werden gerealiseerd. Echter, door de veel hogere kwaliteit van de oxide die vormt op het grensvlak met de atmosfeer, nam silicium de positie van meest gebruikte materiaal in de halfgeleiderindustrie over. Dankzij de opkomst van heterostructuren, waarin de halfgeleider beschermd wordt tussen laagjes van een ander materiaal, is dit tegenwoordig een achterhaald probleem. Zouden daarom de superieure kwaliteiten van germanium een belangrijke rol kunnen gaan spelen in het opkomende quantumtijdperk?

Nico Hendrickx (1994) studeerde technische natuurkunde aan de Universiteit Twente. Na tijdens zijn masteropdracht gewerkt te hebben aan spin-quantumbits in silicium aan de UNSW in Sydney, doet hij nu promotieonderzoek naar spin-quantumbits in germanium bij QuTech aan de TU Delft.

De quantumcomputer wordt misschien wel de heilige graal van deze eeuw. Al sinds de jaren negentig van de vorige eeuw is men er zich van bewust dat bepaalde problemen significant gemakkelijker opgelost kunnen worden wanneer men profiteert van alle mogelijkheden die de quantummechanica ons biedt. Door gebruik te maken van quantumbits, die niet slechts de klassieke toestanden 0 en 1 kennen, maar ook alle mogelijke superposities hiervan, is het mogelijk om problemen op te lossen die binnen een redelijke tijdsduur onoplosbaar zouden zijn op een normale computer. Recent werk van Google laat voor het eerst zien dat een berekening significant sneller uitgevoerd kan worden met een quantumcomputer en onderstreept daarmee diens kracht [1].

Welke quantumbit?
Het is nog niet duidelijk welk fysisch systeem het beste is om de quantumbits in de toekomstige quantumcomputer te vormen. Op dit moment zijn er nog een tiental verschillende kandidaten in competitie, elk met hun eigen voor- en nadelen. Een van de mogelijkheden is de spinquantumbit, waarbij de spreekwoordelijke 0 en 1 bepaald worden door de spin van een elektron of gat in een halfgeleidermateriaal, zoals te zien is op de Blochbol in figuur 1a. In een magneetveld zal de Zeemaninteractie de ontaarding van de spin-omhoog- en spin-omlaagtoestanden van het deeltje opheffen opdat deze de basistoestanden van de quantumbit kunnen vormen. Door middel van elektrostatische elektrodes kan een potentiaallandschap worden gecreëerd waar dit enkele elektron of gat in gevangen kan worden, analoog aan het deeltje in een doos. Een groot voordeel van dit type quantumbits is daarom de kleine fysieke maat van ongeveer 100 bij 100 nanometer, die gedefinieerd wordt door de maat van de elektrodes. Dit betekent dat er ongeveer 42 miljard van dit type quantumbits zouden passen op het oppervlak van een euromunt! Daarnaast zijn de gebruikte elektrodestructuren zeer vergelijkbaar met die van klassieke elektronica en kan men bij de verdere ontwikkeling van grote roosters met spinquantumbits (bijvoorbeeld zoals voorgesteld in figuur 1b) dus profiteren van alle kennis en technieken die de informatierevolutie heeft gebracht.

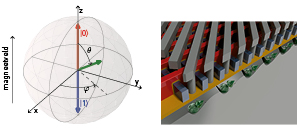
Figuur 1. Links: een quantumbit kan zich in elke mogelijke superpositie van de twee basistoestanden bevinden, zoals te zien op de Blochbol. Rechts: spinquantumbits worden gedefinieerd met metalen elektrodes, vergelijkbaar met de klassieke transistor. Figuur uit [2].

Een tweede kans voor germanium?
Alhoewel germanium werd gebruikt om de eerste transistors en geïntegreerde circuits te bouwen, stapte de industrie al snel over op silicium vanwege de hogere kwaliteit van zijn oxide. Tegenwoordig hebben we echter de technieken om heterostructuren te groeien, waarbij kristallijnlagen van silicium en germanium afgewisseld kunnen worden. Wanneer je op deze manier een dunne laag puur germanium insluit tussen twee dikkere lagen siliciumgermanium (SiGe), gebeurt er iets bijzonders. Het dunne laagje germanium wordt opgerekt door de SiGe en zal diens roosterconstante aannemen. Mede als gevolg hiervan ontstaat er een potentiaalput (quantumput) waarin gaten ingesloten kunnen worden, zoals geschetst links in figuur 2. Op deze manier kunnen we de ladingdragers isoleren van de inferieure oxides aan het grensvlak, om een zeer hoge kwaliteit 2D-kanaal voor gaten te vormen, profiterend van alle kwaliteiten van het germanium. Meer details over de (eigenschappen van de) heterostructuur zijn te vinden in [3].

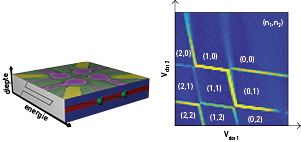
Figuur 2. Links: schematische weergave van de heterostructuur met de elektrodeconfiguratie van een device met vier quantumdots. Links is de bandenstructuur geschetst. Rechts: de respons van de ladingssensor laat de ladingsadditielijnen van quantumdots 1 en 2 zien, die corresponderen met het toevoegen van een enkel gat aan de quantumdot.

Deze gaten in germanium hebben een aantal speciale eigenschappen die gunstig gebruikt kunnen worden bij de definitie van quantumbits. Allereerst ondervinden gaten in het algemeen een sterke spin-baankoppeling, die de spin van het deeltje koppelt aan zijn beweging. Dit opent de mogelijkheid om de spin te roteren met behulp van een elektrisch veld, in tegenstelling tot de situatie van elektronen, waar typisch magneetvelden gebruikt moeten worden. Aangezien de quantumdots gedefinieerd worden met behulp van elektrische velden, is het mogelijk de spins te roteren zonder dat daarvoor extra structuren (zoals micromagneten of transmissielijnen) nodig zijn. Dit is voordelig bij de opschaling naar een groter aantal quantumbits. De keerzijde van de koppeling tussen de spintoestand en elektrische velden is dat elektrische ruis nu ook aan de spintoestand wordt gekoppeld en daarmee een snellere decoherentie veroorzaakt dan in het geval van elektronen. Gelukkig is de rotatiesnelheid van de gatspin typisch ook een stuk hoger, wat de verhoogde decoherentie kan compenseren. Een tweede voordelige eigenschap van germanium is het feit dat het Ferminiveau is vastgepind nabij de rand van de valentieband. Daardoor kan een metaal aan de quantumput gekoppeld worden zonder dat er een grote Schottkybarrière ontstaat. Dit biedt de mogelijkheid om supergeleiders te integreren met de spinquantumbits en op deze manier hybriden te creëren die kunnen profiteren van de voordelen van beide systemen.

Het isoleren van een enkel gat
De heterostructuur zorgt voor een opsluiting van de gaten in de z-richting, maar om een enkel gat op te sluiten, zullen we ook in het xy-vlak een potentiaalput moeten realiseren. Dit doen we met behulp van metalen elektrodes die door middel van elektronenstraallithografie gedefinieerd kunnen worden. Een voorbeeld van een structuur met vier quantumdots is links te zien in figuur 2. Wanneer de ladingdragers op deze manier in alle dimensies ingesloten worden, zal er een ladder van discrete energieniveaus ontstaan door de Coulombafstoting van gelijkgeladen deeltjes en de kwantisatie ten gevolge van de potentiaalput. Alleen als een van deze energieniveaus uitlijnt met het Ferminiveau in de Ohmse contacten, is geleiding door de quantumdot mogelijk. Wanneer de spanning op de quantumdotelektrode gevarieerd wordt, zal de ladder van energieniveaus verschuiven ten opzichte van het Ferminiveau in de Ohmse contacten. Hierdoor zal de geleiding door de dot Coulombpieken tonen, waarbij elke piek correspondeert met het uitlijnen van een nieuw energieniveau tussen de Ohmse contacten. Alhoewel deze meetmethode goed werkt voor een dot met veel gaten, zal het signaal te zwak worden wanneer de quantumdot bijna leeg is en de tunnelsnelheden (en dus de te meten stroom) afnemen. Om het laatste gat toch te kunnen meten, kan een extra quantumdot (met veel gaten) gebruikt worden als ladingssensor. Op de flanken van de Coulombpieken is de geleiding door de quantumdot zeer gevoelig voor een variatie in het elektrisch veld, zoals veroorzaakt door het bewegen van een elektrische lading. Op deze manier kan een quantumdot dus gebruikt worden als een sensor om nabije ladingsbewegingen te detecteren. Wanneer er een gat toegevoegd wordt aan een van de te meten quantumdots, zal die ladingsbeweging een verandering in het lokale elektrisch veld veroorzaken. Dit resulteert vervolgens in een sterke variatie van de sensorgeleiding, die we gemakkelijk kunnen meten. Rechts in figuur 2 laat de sensorrespons zien van de structuur uit paneel a, waarbij twee van de dots de sensor vormen. Er zijn duidelijke horizontale en verticale lijnen zichtbaar, die corresponderen met het toevoegen van een gat aan een van de andere twee dots. In de rechterbovenhoek is te zien dat er geen nieuwe lijnen meer volgen, hetgeen laat zien dat de dots volledig geledigd zijn.

Het meten van de spin
Om dit gat te kunnen gebruiken als een quantumbit, moeten we de spintoestand van het gat natuurlijk ook kunnen uitlezen. Aangezien het magnetisch moment van een enkele spin zeer klein is, is het niet praktisch om dit direct te meten. We maken daarom gebruik van een spin-naar-ladingconversie, waarna we de ladingsbeweging kunnen detecteren zoals eerder beschreven. Een mogelijke methode om dit te doen is Paulispinblokkade, gebaseerd op het uitsluitingsprincipe van Pauli dat stelt dat twee identieke fermionen niet dezelfde quantumtoestand mogen bezetten. Praktisch gezien betekent dit dat twee gelijke spins niet dezelfde quantumdottoestand kunnen bezetten. Door twee gaten uit verschillende quantumdots in dezelfde dot te voegen, kunnen we iets zeggen over de spintoestand van de gaten. In dit geval maken we gebruik van een dubbele quantumdot met een groter aantal gaten, zodat we simpelweg de geleiding van het systeem kunnen meten (maar hetzelfde kan bereikt worden met een ladingssensor). In figuur 3 is geïllustreerd hoe we de energieniveaus van beide dots zo kunnen uitlijnen dat de volgende quantumdottoestand (gestippelde lijn) niet toegankelijk is. In de beschikbare quantumdottoestand in dot 2 bevindt zich al een spin-omlaag. Zodra een spin-omlaag geladen wordt in dot 1 zal het transport stokken, aangezien het gat geen toegankelijke energietoestand heeft in dot 2. Dit zorgt voor een reductie van de transportstroom – te zien aan het missende deel van de driehoek in het diagram rechtsboven.

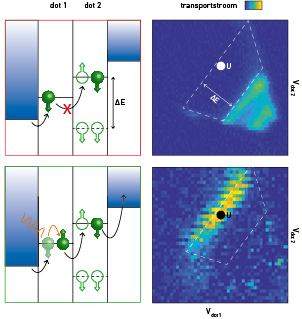
Figuur 3. Paulispinblokkade in een dubbele quantumdot. Door de spin te roteren kan de blokkade opgeheven worden.

Coherente controle van de spin
We zijn in staat de spin te roteren, door een microgolftoon met frequentie gelijk aan de Zeemansplitsing van de spintoestanden aan te bieden op een van de elektrodes. Via de spin-baankoppeling zullen de oscillerende elektrische velden leiden tot een rotatie van de spin. Als gevolg hiervan kan het gat van dot 1 naar dot 2 tunnelen en vervolgens naar het afvoerreservoir. Een nieuwe spin wordt geladen vanuit het bronreservoir en de cyclus begint weer van voor af aan. De blokkade van de transportstroom is daarmee opgeheven, zoals te zien aan de heldere basis van dezelfde driehoek, rechtsonder in figuur 3. Om het contrast te verhogen is hier het verschil in stroom tussen de situatie met microgolf aan en uit weergegeven. Om coherente operaties uit te voeren is deze werkwijze echter niet geschikt. Immers, zodra we de spin hebben geroteerd zal deze wegtunnelen. Om dit te voorkomen kunnen we repeterende spanningspulsen aanbieden op de elektrodes, om de energieniveaus van de dots te verschuiven naar een punt waar ze niet uitlijnen met het Ferminiveau van de reservoirs (Coulombblokkade). We schakelen continu heen en weer tussen het uitleespunt op de basis van de driehoek (punt U in figuur 3) en het manipulatiepunt in de Coulombblokkade. Door nu een microgolfpuls met variabele tijdsduur en fase aan te bieden, kunnen we de spin naar elk willekeurig punt op de Blochbol roteren.

Universele quantumlogica
Om over universele quantumlogica te beschikken, vergelijkbaar aan bijvoorbeeld de NAND-poort voor klassieke logica, hebben we echter nog een ingrediënt nodig: verstrengeling. In het geval van spinquantumbits kunnen we hiertoe gebruikmaken van de exchange-interactie, veroorzaakt door de overlap van de golffuncties van de twee gaten. Deze zorgt voor een verschuiving van de resonantiefrequentie van de ene quantumbit afhankelijk van de toestand van de andere (en vice versa). Dit is te zien in figuur 4, waarin we de resonantiefrequentie van quantumbit 1 (Q1, blauw) meten, waarbij quantumbit 2 (Q2, rood) geprepareerd wordt in de spin-omlaag- en spin-omhoogtoestand in paars en groen respectievelijk. De resonantiefrequentie van Q1 verschuift dus met ongeveer 40 MHz, afhankelijk van de staat van Q2. Door een microgolfpuls aan te bieden met frequentie f1 of f2, is het mogelijk een conditionele rotatie van Q1 uit te voeren en de benodigde verstrengeling te creëren. Zoals te zien in figuur 4, zijn we in staat een dergelijke conditionele rotatie uit te voeren in slechts zeventig nanoseconden. Gecombineerd met de (eveneens snelle) enkele-quantumbitrotaties, maakt dit het uitvoeren van snelle universele quantumlogica mogelijk.

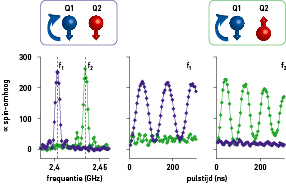
Figuur 4. Conditionele rotatie van quantumbit 1 (Q1), afhankelijk van de toestand van quantumbit 2 (Q2), complementeert de universele quantumlogica. Figuur aangepast uit [4].

We hebben daarmee alle benodigde ingrediënten voor quantumcomputatie met spinquantumbits in germanium gedemonstreerd. Daarnaast zien we dat gaten in germanium enkele bijzondere eigenschappen hebben, zoals de sterke spin-baankoppeling en de mogelijkheid om supergeleiders te integreren in het halfgeleiderplatform. Dit biedt de mogelijkheid om de quantumbits snel en lokaal te sturen en opent de weg naar het ontwikkelen van hybride spinquantumbitsupergeleidertoepassingen. Germanium was het materiaal dat het informatietijdperk ontketende en zou dankzij zijn bijzondere kwaliteiten een belangrijke rol kunnen gaan spelen in de quantumrevolutie.

Referenties
1 F. Arute et al., Nature 574, 505 (2019).
2 R. Li et al., Science Advances 4, 7 (2018).
3 A. Sammak et al., Advanced Functional Materials 29, 14 (2019).
4 N. Hendrickx et al., Nature 557, 487-491 (2020).